【初中数学】数与代数公式汇编

【来源：点金教育一对一个性化辅导数学组 张继同】

点金教育中考签约提分保过班开始报名了，考上泰安一中、泰安二中等理想学校已不再是想想而已，详情点击查看详情… …

1.数与式

(1)实数

实数的性质：

①实数a的相反数是—a，实数a的倒数是（a≠0）；

②实数a的绝对值：

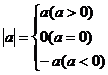
③正数大于0，负数小于0，两个负实数，绝对值大的反而小。

二次根式：

①积与商的方根的运算性质：

（a≥0，b≥0）；

（a≥0，b＞0）；

②二次根式的性质：

(2)整式与分式

整式

①同底数幂的乘法法则：同底数幂相乘，底数不变，指数相加，即（m、n为正整数）；

②同底数幂的除法法则：同底数幂相除，底数不变，指数相减，即（a≠0，m、n为正整数，m>n）；

③幂的乘方法则：幂的乘方，底数不变，指数相乘，即（n为正整数）；

④零指数：（a≠0）；

⑤负整数指数：（a≠0，n为正整数）；

⑥平方差公式：两个数的和与这两个数的差的积等于这两个数的平方，即；

⑦完全平方公式：两数和（或差）的平方，等于它们的平方和，加上（或减去）它们的积的2倍，即；

分式

①分式的基本性质：分式的分子和分母都乘以（或除以）同一个不等于零的整式，分式的值不变，即；，其中m是不等于零的代数式；

②分式的乘法法则：；

③分式的除法法则：；

④分式的乘方法则：（n为正整数）；

⑤同分母分式加减法则：；

⑥异分母分式加减法则：；

2.方程与不等式

一元二次方程

①一元二次方程(a≠0）的求根公式：

②一元二次方程根的判别式：叫做一元二次方程（a≠0）的根的判别式：

方程有两个不相等的实数根；方程有两个相等的实数根；

方程没有实数根；

③一元二次方程根与系数的关系：设、是方程 （a≠0）的两个根，那么+=，=；

不等式的基本性质：

①不等式两边都加上（或减去）同一个数或同一个整式，不等号的方向不变；

②不等式两边都乘以（或除以）同一个正数，不等号的方向不变；

③不等式两边都乘以（或除以）同一个负数，不等号的方向改变；

3.函数

一次函数

一次函数的图象：函数y=kx+b(k、b是常数，k≠0)的图象是过点（0，b）且与直线y=kx平行的一条直线；

一次函数的性质：设y=kx+b（k≠0），则当k>0时，y随x的增大而增大；当k<0， y随x的增大而减小；

正比例函数

正比例函数的图象：函数的图象是过原点及点（1，k）的一条直线。

正比例函数的性质：设，则：

①当k>0时，y随x的增大而增大；

②当k<0时，y随x的增大而减小；

反比例函数

反比例函数的图象：函数（k≠0）是双曲线；

反比例函数性质：设（k≠0），如果k>0，则当x>0时或x<0时，y分别随x的增大而减小；如果k<0，则当x>0时或x<0时，y分别随x的增大而增大；

二次函数

二次函数的图象：函数的图象是对称轴平行于y 轴的抛物线；

①开口方向：当a>0时，抛物线开口向上，当a<0时，抛物线开口向下；

②对称轴：直线；

③顶点坐标（；

④增减性：当a>0时，如果，则y随x的增大而减小，如果，则y随x的增大而增大；当a<0时，如果，则y随x的增大而增大，如果，则y随x的增大而减小.