泰安市泰山区六年级数学期中考试对策

泰安市泰山区六年级数学期中考试对策

一、知识梳理

第一章 丰富的图形世界

1、常见的几何体及其特点

(1)长方体：有8个顶点，12条棱，6个面，且各面都是长方形（正方形是特殊的长方形）正方体是特

           殊的长方体。

(2)棱柱：上下两个面称为棱柱的底面，其它各面称为侧面，长方体是四棱柱。

(3)圆柱：有上下两个底面和一个侧面，两个底面是半径相等的圆。

(4)圆锥：有一个底面和一个顶点，且侧面展开图是扇形。

(5)球：由一个面围成的几何体。

2、展开与折叠

(1)棱柱：如图1所示的棱柱，上底面是五边形A＇Ｂ＇Ｃ＇Ｄ＇Ｅ＇，下底面是五边形ABCDE，这两个五边形的大小形状都相同，这个棱柱有5个侧面，当它为直棱柱时，5个侧面都是长方形，当它为斜棱柱时，5个侧面都是平行四边形，在棱柱中任何相邻的两个面的交线都叫做棱柱的棱，其中相邻的两个侧面的交线都叫做棱柱的侧棱，图1中的棱柱有15条棱，其中有5条侧棱，这5条侧棱的长相等，将这个棱柱展开定一个长方形（图2是图1中棱柱的侧面展开图）反过来可以将一个长方形折叠成一个棱桂的侧面。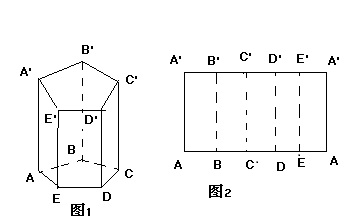

 

    当一个棱柱的地面是三角形时，称为三棱柱，当一个棱柱的底面是四边形时，称为四棱柱，（长方体正方体都是四棱柱）当一个棱柱的底面是五边形时，称为五棱柱（图1就是五棱柱）………当一个棱柱的底面是n边形时，称为n棱柱，它有2n个顶点，3n条棱，(n十2)个面（其中2个底面，n个侧面）。

(2)圆柱和圆锥的侧面展开图：圆柱的侧面展开图是一个长方形，圆柱的底面周长   和高分别是这个长方体的长与宽，圆锥的侧面展开图是一个扇形，这个扇形的半径就是圆锥的母线（即圆锥的顶点与圆锥底面上任意一点的连线长，而扇形的弧长就是圆锥底面圆的周长，反过来，可以将一个扇形围成一个圆锥的侧面。

3、截一个几何体

(1)用一个截面去截长方体或正方体，截面可能是等腰三角形、等边三角形、但不可能是直角三角形，也可能是正方形，长方形，梯形，五边形等，最多可截得六边形。

(2)用一个截面去截圆柱，截面可能是正方形，长方形，梯形、圆或椭圆。

(3)用一个截面去截圆锥，截面可能是等腰三角、圆、抛物线形或椭圆。

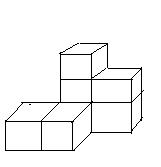
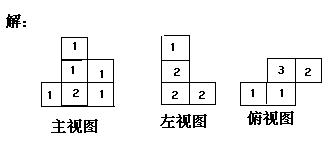
4、三视图

    我们从不同方向观察物体时，从正面看到的图形叫做主视图，从左边看到的图形叫做左视图，从上面看到的视图叫做俯视图。

如图左边是一个由小立方块组成的几何体，右边是这个几何体的三种视图。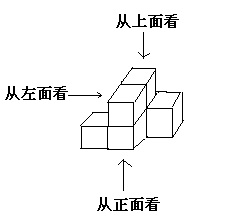

 

5、认识生活中的平面图形

我们生活中所见的平面图形有：三角形、四边形、五边形、圆等。其中多边形是由一些不在同一直线上的线段依次首尾相连组成的封闭图形。圆上两点之间的部分叫做弧，由一条弧和经过这条弧的端点的两条半径所组成的图形叫做扇形。设一个多边形的边数为n，从这个n边形的一个顶点出发，分别连接这个项点与n边形的其它各项点（与这个项点相邻的顶点除外，）可以得到（n一3）条对角线，（n一2）个三角形，一个圆可以被它的半径分割成若干个扇形。

第二章 有理数及其运算

                      

   

2、数轴的三要素：原点、正方向、单位长度（三者缺一不可）。

3、任何一个有理数，都可以用数轴上的一个点来表示。（反过来，不能说数轴上所有的点都表示有理数）

4、如果两个数只有符号不同，那么我们称其中一个数为另一个数的相反数，也称这两个数互为相反数。

  （0的相反数是0）

5、在数轴上，表示互为相反数的两个点，位于原点的两侧，且到原点的距离相等。

   数轴上两点表示的数，右边的总比左边的大。正数在原点的右边，负数在原点的左边。

6、绝对值的定义：一个数a的绝对值就是数轴上表示数a的点与原点的距离。数a的绝对值记作|a|。

7、正数的绝对值是它本身；负数的绝对值是它的相反数；0的绝对值是0。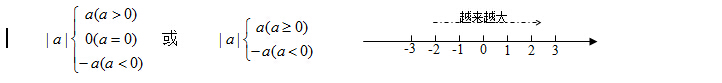

8、绝对值的性质：除0外，绝对值为一正数的数有两个，它们互为相反数；

   互为相反数的两数（除0外）的绝对值相等；

   任何数的绝对值总是非负数，即|a|≥0。

9、比较两个负数的大小，绝对值大的反而小。比较两个负数的大小的步骤如下：

   ①先求出两个数负数的绝对值；

 ②比较两个绝对值的大小；

 ③根据“两个负数，绝对值大的反而小”做出正确的判断。

10、绝对值的性质：

    ①对任何有理数a，都有|a|≥0

    ②若|a|=0，则|a|=0，反之亦然

    ③若|a|=b，则a=±b

    ④对任何有理数a,都有|a|=|-a|

11、有理数加法法则：

①同号两数相加，取相同符号，并把绝对值相加。

②异号两数相加，绝对值相等时和为0；绝对值不等时取绝对值较大的数的符号，并用较大数的

  绝对值减去较小数的绝对值。

    ③一个数同0相加，仍得这个数。

12、加法的交换律、结合律在有理数运算中同样适用。灵活运用运算律，使用运算简化，通常有下列规

    律：①互为相反的两个数，可以先相加；

        ②符号相同的数，可以先相加；

        ③分母相同的数，可以先相加；

       ④几个数相加能得到整数，可以先相加。

13、有理数减法法则： 减去一个数，等于加上这个数的相反数。有理数减法运算时注意两“变”：

    ①改变运算符号；

    ②改变减数的性质符号（变为相反数）

    有理数减法运算时注意一个“不变”：被减数与减数的位置不能变换，也就是说，减法没有交换律。

14、有理数的加减法混合运算的步骤：

①写成省略加号的代数和。在一个算式中，若有减法，应由有理数的减法法则转化为加法，然后再

      省略加号和括号；

    ②利用加法则，加法交换律、结合律简化计算。

   （注意：减去一个数等于加上这个数的相反数，当有减法统一成加法时，减数应变成它本身的相反

    数。）

15、有理数乘法法则：

    ①两数相乘，同号得正，异号得负，并把绝对值相乘。

    ②任何数与0相乘，积仍为0。

    如果两个数互为倒数，则它们的乘积为1。（如：2与 、 …等）

16、乘法的交换律、结合律、分配律在有理数运算中同样适用。

有理数乘法运算步骤：

①先确定积的符号；

    ②求出各因数的绝对值的积。

    乘积为1的两个有理数互为倒数。注意：

    ①零没有倒数；

    ②求分数的倒数，就是把分数的分子分母颠倒位置。一个带分数要先化成假分数；

    ③正数的倒数是正数，负数的倒数是负数。

 17、有理数除法法则：

    ①两个有理数相除，同号得正，异号得负，并把绝对值相除。

    ②0除以任何非0的数都得0。0不可作为除数，否则无意义。

 18、有理数的乘方    

    注意：①一个数可以看作是本身的一次方，如5=5¹；

          ②当底数是负数或分数时，要先用括号将底数括上，再在右上角写指数。

 19、乘方的运算性质：

    ①正数的任何次幂都是正数；

    ②负数的奇次幂是负数，负数的偶次幂是正数；

    ③任何数的偶数次幂都是非负数；

    ④1的任何次幂都得1，0的任何次幂都得0；

    ⑤-1的偶次幂得1；-1的奇次幂得-1；

    ⑥在运算过程中，首先要确定幂的符号，然后再计算幂的绝对值。

 20、有理数混合运算法则：

    ①先算乘方,再算乘除,最后算加减。

②如果有括号,先算括号里面的。

二、典型例题

1、亲身经历切截正方体的过程，体会面与体的转换，提高动手操作能力。

例1 用一个平面去截正方体，能得两边相等、三边相等的三角形吗？能截出长方形与梯形吗？

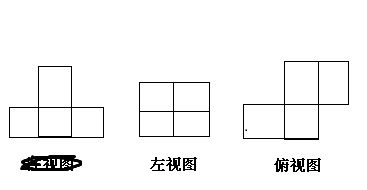
2、从不同方向观察同一物体，画出三视图，并在小正方形内填上表示说位置小立方块的个数。

例2  画出下列立方体的三视图，并在该位置填上小立方块的个数。

 

                             

3、有理数的概念

例3 如果a的相反数是2，那么a等于（    ）

     A、-2     B、2     C、     D、-

例4 有理数-的倒数是（    ）

     A、-2     B、2     C、     D、-

例5 数轴上的点A到原点的距离是6，则点A表示的数为（    ）

A、6或-6     B、6     C、-6     D、3或-3

4、有理数的计算

例6 计算2+|-1|-3

例7 3×3.14+3×(-9.42)=      .

5、近似数与科学记数法

例8 某地区有54 310人参加中考，将54 310用科学记数法表示为（    ）(精确到千位)

    A、54×10     B、0.54×10     C、5.4×10     D、5.5×10

6、有理数的运算规律探索

例9 观察下列等式：3=3,3=9,3=27,3=81,3=243，…，解答下列问题：3+3+3+3+…+3的末位数字是（    ）

     A、0     B、1     C、3     D、7